목차
바둑에서의 역끝내기
TV 해설을 듣다 보면 "여기는 역끝내기 7집이니까 두 배, 그러니까 14집 크기거든요." 같은 소리를 들으며 의아해하실 분들이 있을 겁니다. 7집이면 7집이지 왜 두 배 크기인가? 게다가 양선수 끝내기는 4배 크기라니? 이런 분들을 위해 왜 역끝내기의 크기를 두 배로 치는지 간단히 짚어 보겠습니다. 다음과 같은 상황을 생각해 봅시다.
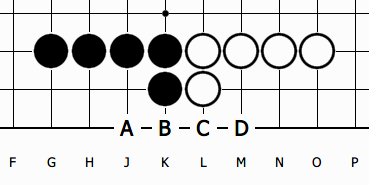
이것은 양후수 끝내기입니다. 흑이 C로 젖혀잇는다면 A의 곳에 집이 생기고, 백이 B로 젖혀이으면 D의 곳에 백집이 생기며, 서로 후수 끝내기입니다. A~D까지의 곳에 집이 얼마나 생기는지 다시 정리해 보면-
| 흑집 | 백집 | |||
| 흑이 끝내기할 경우 |
1(A) | 0 | ||
| 백이 끝내기할 경우 |
0 | 1(D) | ||
따라서, 두 경우의 크기는 2집 차이이고, 그러므로 2집 크기의 끝내기가 됩니다. (안팎 계산법) 형세판단할 때는, 권리가 반반이므로 보통 B에 흑돌, C에 백돌이 있다고 가정합니다. 즉, 흑은 A에 한집, 백은 D에 한집이 있다고 세는 거죠. 하지만 기대값 측면에서는 조금 다릅니다.
이 끝내기의 권리는 흑백이 각각 반씩 나누어 가지고 있습니다. 동일한 권리를 가진 것이죠. 확률적으로 얘기한다면, 각각 1/2의 확률이고, 기대값을 계산한다면-
기대값 = 집의 크기(흑이 끝내기) * 흑이 끝내기할 확률 + 집의 크기(백이 끝내기) * 백이 끝내기할 확률
흑집의 기대값 = 1 * (1/2) + 0 * (1/2) = 1/2
백집의 기대값 = 0 * (1/2) + 1 * (1/2) = 1/2
즉, 흑은 A의 곳에 반집, 백은 D의 곳에 반집이 있다고 생각하는 것입니다. 물론 서로 한 집씩 있다고 보아도 집차이에는 아무런 영향이 없으므로 형세판단할 때는 상관이 없습니다만...
이 경우 흑이 끝내기를 한다면, 흑집과 백집이 각각 1/2이던 상황에서 흑집은 1집, 백집은 0집으로 확정이 됩니다. 기대값과 비교할 때, 흑집은 1/2집, 백집은 1/2집 차이가 나므로 합해서 1집 차이가 나겠네요. (기대값 기준 계산법) 이 경우, 안팎 계산법에 비해 끝내기의 가치가 절반으로 줄어들었습니다만, 이것은 계산법의 차이에 따라 이렇게 된 것입니다.
반면 다음의 끝내기를 볼까요.
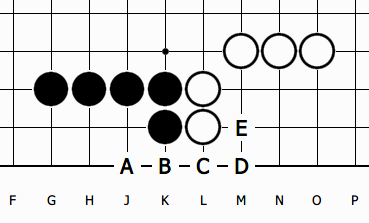
| 흑집 | 백집 | |||
| 흑이 끝내기할 경우 |
1(A) | 0 | ||
| 백이 끝내기할 경우 |
0 | 2(D, E) | ||
즉, 집차이는 총 3집이고, 흑 입장에서는 선수 끝내기 3집, 백 입장에서는 역끝내기 3집이 됩니다. (안팎 계산법)
형세판단할 때는 흑이 권리를 가진 끝내기이므로 흑이 C로 젖혀이었다고 가정하고 집을 세게 됩니다. 그럼 기대값은 어떻게 될까요? 흑이 권리를 가졌으므로, 흑이 끝내기할 확률이 1이고, 백이 끝내기할 확률은 0으로 봅니다. (=흑의 권리라는 말과 사실상 동일)
기대값 = 집의 크기(흑이 끝내기) * 흑이 끝내기할 확률 + 집의 크기(백이 끝내기) * 백이 끝내기할 확률
흑집의 기대값 = 1 * (1) + 0 * (0) = 1
백집의 기대값 = 0 * (1) + 2 * (0) = 0
이 결과는, 흑이 젖혀이었다고 가정한 그대로입니다. 흑집과 백집의 기대값은 각각 1집, 0집이고, 흑이 끝내기하면 1집, 0집이 되며 백이 끝내기하면 0집, 2집이 되므로, 기대값 기준으로 계산했을 때 끝내기의 크기는 3집입니다.
그럼 여기서 다시 정리해 볼까요.
| 양후수 끝내기 |
편선수 끝내기(역끝내기) |
|
| 안팎 계산법 |
2집 | 3집 |
| 기대값 기준 계산법 |
1집 | 3집 |
양후수 끝내기의 경우, 두 계산법에 2배의 크기 차이가 나는 반면, 편선수 끝내기는 차이가 없습니다. 어느 쪽을 믿어야 할까요? 정답은 기대값 기준 계산법입니다.
양후수끝내기의 경우, 형세판단할 때 각각 1집씩 나 있다고 가정한 상황에서, 흑이 끝내기를 한다면 흑집은 그대로이고 백집은 1집 줄었으니, 흑이 1집을 이득보았습니다. 따라서 실질적으로는 1집 크기의 끝내기라 할 수 있습니다. 그러므로 실제로 양후수 끝내기 2집짜리는 1집 크기라 할 수 있습니다. 다만 안팎 계산법이 계산하기 편한 측면이 있고, 1/4집, 1/8집, 1/12집 등을 말하기 귀찮으므로 편의상 2집 끝내기라고 말하는 것입니다. 따라서, "왜 역끝내기의 크기는 두 배일까?"보다는, "왜 양후수 끝내기의 크기는 절반일까?"가 사실은 옳다고 할 수 있겠습니다.
마지막으로 양선수 끝내기를 살펴볼까요.
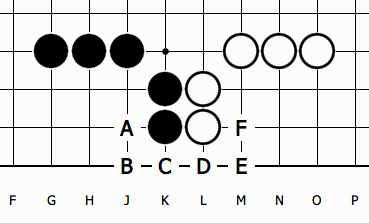
흑이 D로 젖혀잇는 것도, 백이 C로 젖혀잇는 것도 선수이고, 흑은 A, B에, 백은 E, F에 2집씩 증감하므로,
| 흑집 | 백집 | |||
| 흑이 끝내기할 경우 |
2(A, B) | 0 | ||
| 백이 끝내기할 경우 |
0 | 2(E, F) |
집차이는 총 4집, 양선수 끝내기입니다. (안팎 계산법) 자, 근데 역끝내기의 크기가 2배인 건 알겠는데, 왜 양선수 끝내기의 크기는 4배일까요? 이는 지금 누가 둘 차례인가와 밀접한 관련이 있습니다.
지금 흑이 둘 차례고, 흑이 저 끝내기를 할 수 있는 국면이라면, 저곳은 흑의 권리가 됩니다.
반면, 흑이 다른 양후수 끝내기나 역끝내기를 서둘렀다면, 저곳은 백의 권리가 되겠죠.
다르게 말해,
흑선이면 기대값은 흑집 2집, 백집 0집이 되고,
백선이면 기대값은 흑집 0집, 백집 2집이 됩니다.
즉, 선수권리를 포기하고 다른 곳에 둠으로 인해 기대값만 4집(끝내기의 크기)이 날아가는 거죠. 여기에 끝내기의 크기 4집을 더하면 총 8집의 크기라 볼 수 있겠습니다. 그러므로 양선수 끝내기는 둘 수 있으면 서둘러 마치는 것이 무조건 옳습니다.
여태 역끝내기의 크기가 왜 두 배인지 설명했습니다. 그러면, 기대값 기준 계산법에 의거해서 큰 곳부터 두면 되느냐? 그건 또 아닙니다. 지금 흑선이라고 가정하고, 반상에 남은 끝내기는 다음과 같이 셋뿐이라고 생각해 봅시다.
역끝내기 5집, 양후수 9집, 양후수 3집
여기서, 기대값 기준 계산법에 의하면, 끝내기의 크기는 5집, 4.5집, 1.5집이라고 해서 역끝내기를 서두르면-
흑: 역끝내기 5집
백: 양후수 9집
흑: 양후수 3집
흑 총 8집 획득, 백 총 9집 획득
반면, 흑이 양후수 9집 끝내기를 둔다면-
흑: 양후수 9집
백: 편선수 5집
백: 양후수 3집
흑 총 9집 획득, 백 총 8집 획득
(이 경우는 안팎 계산법을 적용하는 것이 정확한데, 왜 그런지는 생략합니다)
오히려 두 배 크기라고 믿었던 역끝내기를 서두르는 것이 손해가 됩니다. 따라서 기대값 기준 계산법만 믿다가는 뒤통수를 얻어맞는 일이 생기므로, 언제 역끝내기를 해야 할지 잘 생각해 봐야 합니다. 이와 유사한 경우에는-
역끝내기 A집, 양후수 B집, 양후수 C집일 때 (B > A > C)
A + C > B이면 역끝내기를 해도 좋습니다.
왜냐? 내가 양후수 B집을 차지하면 상대가 A, C를 차지하고
내가 역끝내기 A집을 차지하면 상대가 B, 내가 C집을 차지하니까.
이걸로 글을 마치도록 하겠습니다. 끝내기는 참 어려운 거 같아요. 특히 실전에서 집을 정확하게 계산하고 지금 남아 있는 끝내기를 크기별로 나열한다든가 하는 것은 참 어렵고, 또 뒷맛 관계나 팻감이 얽혀 있거나, 혹은 손해를 보고 선수를 잡아야 할 때, 이런 게 얽히면 정말 머리가 아픕니다. 그러므로 저는 끝내기를 하기 전에 상대를 끝내는 방향으로 바둑을 둘까 합니다.
'바둑' 카테고리의 다른 글
| 바둑에서 많이 사용하는 눈목자 받음 뜻과 설명 (0) | 2023.05.15 |
|---|---|
| 바둑 용어 정리(삼단젖힘, 오궁도화, 옥집활) (0) | 2023.05.15 |
| 바둑 책 추천 (초보자부터 상급자까지) (0) | 2023.05.15 |
| 바둑 사이트 장단점 비교 분석(넷마블 바둑, 타이젬) (0) | 2023.05.15 |
| 바둑과 관련된 사자성어 10가지 (0) | 2023.05.13 |

